Multiple-continuum processing
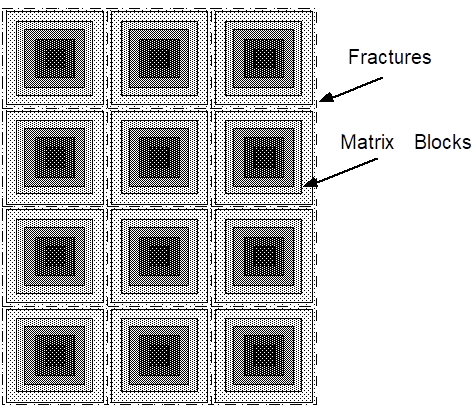
Multiple-continuum processing for simulation of flow in naturally fractured reservoirs can be invoked by means of a keyword MINC, which stands for “multiple interacting continua” (Pruess and Narasimhan, 1982, 1985). The MINC-process operates on the data of the primary (porous medium) mesh as provided on file MESH, and generates a “secondary” mesh containing fracture and matrix elements with identical data formats on file MINC. By appropriate subgridding of the matrix blocks, as shown in Figure 28, and therefore by resolving the driving pressure, temperature, and mass fraction gradients at the matrix and fracture interface, the transient, multiphase interporosity flows between rock matrix and fractures can accurately be described. The MINC concept is based on the notion that changes in fluid pressures, temperatures, phase compositions, etc. due to the presence of sinks and sources (production and injection wells) will propagate rapidly through the fracture system, while invading the tight matrix blocks only slowly. Therefore, changes in matrix conditions will (locally) be controlled by the distance from the fractures. Fluid and heat flow from the fractures into the matrix blocks, or from the matrix blocks into the fractures, can then be modeled by means of one-dimensional strings of nested grid blocks, as shown in Figure 28. The MINC-method lumps all fractions within a certain reservoir subdomain into continuum # 1, all matrix material within a certain distance from the fractures into continuum # 2, matrix material at larger distance into continuum # 3, and so on. Quantitatively, the subgridding is specified by means of a set of volume fractions, into which the primary porous medium grid blocks are partitioned. The MINC-process in the MESHMaker module operates on the element and connection data of a porous medium mesh to calculate, for given data on volume fractions, the volumes, interface areas, and nodal distances for a secondary fractured medium mesh. The information on fracturing (spacing, number of sets, shape of matrix blocks) required for this is provided by a “proximity function” PROX(x) which expresses, for a given reservoir domain Vo, the total fraction of matrix material within a distance x from the fractures. If only two continua are specified (one for fractures, one for matrix), the MINC approach reduces to the conventional double-porosity method (Warren and Root, 1963). Full details are given in a separate report (Pruess, 1983). For any given fractured reservoir flow problem, selection of the most appropriate gridding scheme must be based on a careful consideration of the physical and geometric conditions of flow. The MINC approach is not applicable to systems in which fracturing is so sparse that the fractures cannot be approximated as a continuum.
The file MESH used in this process can be either directly supplied by the user, or it can have been internally generated either from data in input blocks ELEME and CONNE, or from RZ2D or XYZ mesh- making. The MINC process of sub-partitioning porous medium grid blocks into fracture and matrix continua will only operate on active grid blocks, while inactive grid blocks are left unchanged as single porous medium blocks. In TOUGH4, elements in data block ELEME (or file MESH) are taken to be “active” unless they are specified as "inactive" or have very large volumes, which are taken to be “inactive.” In order to exclude selected reservoir domains from the MINC process and make them remain single porous media, the user needs to change the volume of the corresponding blocks to a very large number before MINC partitioning is made. Note that here the concept of inactive blocks is used in an unrelated manner with respect to the one to maintain time-independent Dirichlet boundary conditions.